Apêndice C - Força de Coriolis:

A força de Coriolis surge como conseqüência de observarmos os movimentos do ar num sistema de coordenadas não inercial, isto é, um sistema de coordenadas fixo sobre a superfície, que gira com ela.

As leis de Newton do movimento são válidas para sistemas de referência inerciais (sem aceleração). Para usá-las num sistema não inercial pode-se adaptar as leis de Newton introduzindo forças fictícias. A conexão entre uma aceleração observada de um sistema inercial,  , e aquela observada de um sistema não inercial,  , é dada por:

onde a aceleração fictícia,  , é dada por
 

sendo A a aceleração do sistema não inercial. A (7.4) pode ser escrita em termos de forças, multiplicando-se os termos pela massa:
 

Considerando-se parcelas de massa unitária, a (7.4) e (7.6) são numericamente iguais.

        Um exemplo de fácil compreensão é o de um passageiro fixo a um carro que descreve uma curva circular de raio r, com velocidade  . Um observador externo constata que o carro e o passageiro estão submetidos a uma aceleração centrípeta que muda continuamente a direção de sua velocidade (Fig. 7.3) e que é dada por

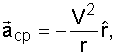
onde  é o vetor unitário dirigido do centro para o carro.

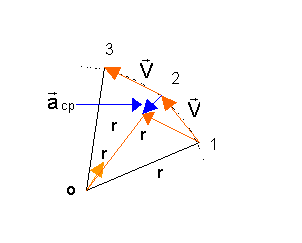
Fig. 7.3 - Corpo em trajetória circular.

O corpo passa de 1 para 2 e de 2 para 3 em intervalos de tempo unitários.

O passageiro fixo ao carro está, contudo, em repouso em relação a um sistema de coordenadas também fixo ao carro. Para expressar esta condição de repouso (ou força resultante nula), usando as leis de Newton, é necessário adotar a existência de uma aceleração centrífuga,  :

tal que a força resultante seja nula:

No caso do movimento do ar segundo um sistema de coordenadas que gira junto com a Terra (Fig. 7.4), aparecem duas forças fictícias: a força centrífuga e a força de Coriolis. A força centrífuga vai alterar a força de atração gravitacional verdadeira entre a parcela de ar e a Terra, produzindo a gravidade efetiva ou gravidade.

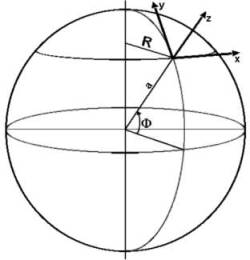
Fig. 7.4 - Sistema de coordenadas fixo à Terra

A força de Coriolis só atua sobre corpos (no nosso caso, parcelas de ar) em movimento em relação ao sistema fixo à Terra e sempre em direção perpendicular ao movimento, de modo a alterar apenas a direção do movimento. Já a força centrífuga atua também sobre corpos fixos em relação à Terra.

        Vamos mostrar como a força de Coriolis devida ao movimento em relação à Terra pode ser obtida num caso particular, considerando uma parcela de ar movendo-se de oeste para leste com velocidade u em relação à Terra, cuja velocidade angular de rotação é

  .

Do ponto de vista de um observador externo à Terra, num sistema inercial, a parcela está se movendo ao longo de uma trajetória circular com velocidade

onde R é a distância ao eixo de rotação da terra (fig. 7.4) e W R é a velocidade tangencial do sistema de coordenadas. Como a parcela está se movendo num círculo de raio R, com velocidade (W R+u), ela tem uma aceleração centrípeta dada por:

.

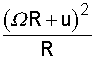Para um observador que gira junto com a Terra, a aceleração aparente em direção ao eixo da Terra é apenas u²/R. No entanto, a soma das forças reais, , por unidade de massa, é, segundo a 2ª lei de Newton, aplicada pelo observador inercial:
 

onde  é o vetor unitário perpendicular ao eixo de rotação, dirigido do eixo para parcela. Portanto, para que o observador que gira com a Terra possa aplicar a 2ª lei de Newton, é necessário introduzir duas forças aparentes por unidade de massa:
 

que modifica a força gravitacional, e
 

A força de Coriolis pode ser decomposta em dois componentes, conforme a figura 7.5:
 

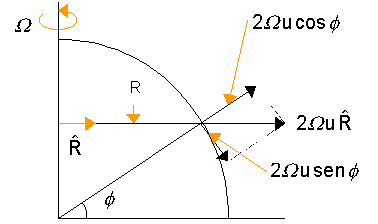
Fig. 7.5 - Componentes da força de Coriolis devida ao movimento relativo ao longo de um círculo de latitude.

O componente vertical é muito menor que a força gravitacional, de modo que ele afeta muito pouco os movimentos verticais.

Podemos também obter a expressão do componente horizontal da força de Coriolis para o caso de um movimento da parcela em relação à Terra na direção sul-norte, com velocidade v. Não vamos mostrar aqui esta dedução. Neste caso, a força de Coriolis é dada por:
 

De maneira geral, pode-se dizer-se que o componente horizontal da força de Coriolis é dado por
 

e é sempre perpendicular à direção do movimento, induzindo desvio para a direita no Hemisfério Norte e para a esquerda no Hemisfério Sul. Estes desvios em relação a um sistema fixo à Terra podem ser exemplificados de maneira simples. Comumente define-se
 

Imaginemos um foguete lançado do Polo Norte para um alvo no equador (Fig. 7.6). Se o foguete leva 1 hora para atingir o alvo, a Terra terá girado 15° para leste durante o vôo. Para alguém fixo sobre a Terra pareceria que o foguete desviou sua rota e atingiu a Terra 15° a oeste de seu alvo. Na realidade, a trajetória do foguete foi reta e assim seria vista por um observador fixo no espaço. Foi a rotação da Terra que produziu, para um observador na Terra, a aparente deflexão. Note que o foguete foi desviado para a direita de seu percurso devido à rotação anti-horária do HN (visto do espaço). Rotação horária do HS (visto do espaço) produz desvio para a esquerda.

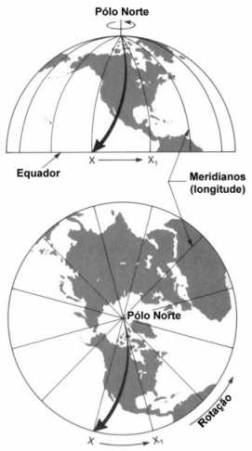
Fig. 7.6 - O efeito de Coriolis. Durante o vôo do foguete do Polo Norte ao ponto x, a rotação da Terra levou o ponto x à posição x₁. A rotação da Terra faz com que a trajetória do foguete assinalada sobre a superfície da Terra seja curva.

Embora seja usualmente fácil visualizar o efeito de Coriolis quando o movimento é do norte para o sul, não é tão fácil ver como um vento de oeste para leste seria desviado. A figura 7.7 ilustra esta situação, mostrando um vento que sopra para leste ao longo do paralelo 40° S, Algumas horas depois, o que era vento oeste transformou-se em vento noroeste no HN e sudoeste no HS, em relação ao sistema de coordenadas fixo à Terra.

Como se vê pela (7.15) a força de Coriolis depende da velocidade do vento, isto é, o desvio é maior se a velocidade for maior. Isto ocorre porque, no mesmo período de tempo, parcelas de ar mais rápidas percorrem distâncias maiores que parcelas mais lentas. Quanto maior o deslocamento, maior o desvio do sistema de coordenadas em relação à parcela de ar.

Também da (7.15) se constata que a força de Coriolis depende da latitude, sendo nula no equador e máxima nos pólos. Isto ocorre porque a força de Coriolis provém da rotação da Terra sobre seu eixo, que produz uma rotação do sistema de referência fixo à Terra. A rotação do nosso sistema de referência é máxima nos pólos e diminui com a latitude, até anular-se no equador. Isto pode ser visualizado na figura 7.8. Nos pólos, onde a superfície é perpendicular ao eixo da Terra, a rotação diária faz com que o plano horizontal do nosso sistema de coordenadas faça uma volta completa em torno do eixo vertical cada 24 horas. Em outras palavras, a superfície sobre a qual o vento sopra faz uma rotação completa cada dia. No equador a superfície da Terra é paralela ao eixo de rotação da Terra; conseqüentemente, ela não sofre rotação em torno de um eixo vertical à superfície. Portanto, no equador a superfície sobre a qual o vento sopra não sofre rotação num sentido horizontal. A diferença pode ser facilmente visualizada se imaginarmos um poste vertical situado no Polo Norte e um situado no equador. Durante o curso de um dia o poste sobre o Polo faz uma rotação completa sobre seu eixo vertical, mas o poste situado no equador não gira sobre si, e apenas coincidirá com sua posição inicial. Os postes situados entre estes extremos experimentam taxas intermediárias de rotação em torno de seus eixos verticais. Conseqüentemente, como a orientação horizontal (rotação em torno de um eixo vertical) da superfície da Terra muda mais rapidamente em altas latitudes que em baixas latitudes, a força de Coriolis será maior em altas latitudes.

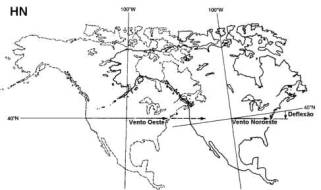
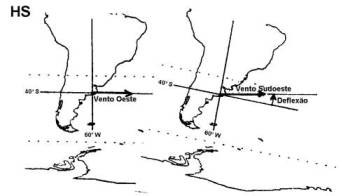
Deflexão de Coriolis sobre um vento oeste. Após algumas horas a rotação da Terra muda a posição da superfície sobre a qual o vento sopra, causando a deflexão aparente.

A força desviadora é omissível para movimentos cujas escalas de tempo são muito pequenas comparadas ao período de rotação da Terra. Assim, a força de Coriolis não é importante para a dinâmica de nuvens cumulus individuais, mas é essencial para a compreensão de fenômenos de escala de tempo maior, tais como sistemas de escala sinótica. Por isso, não tem fundamento a crença de que a rotação da água que escoa numa pia ou banheira ocorra consistentemente numa direção no Hemisfério Norte e na direção oposta no Hemisfério Sul, presumivelmente devido ao efeito de Coriolis. Nesta pequena escala de tempo a magnitude do efeito de Coriolis é muito pequena para ter um efeito significativo sobre a direção de rotação. A direção de rotação neste caso é mais provavelmente conseqüência de algum movimento residual da água antes de escoar.

Para ter uma idéia da magnitude da força de Coriolis, consideremos na (7.15) os seguintes valores:

.

Comparando este valor com o obtido para a força do gradiente de pressão, pode-se concluir que é possível obter um balanço entre essas forças.

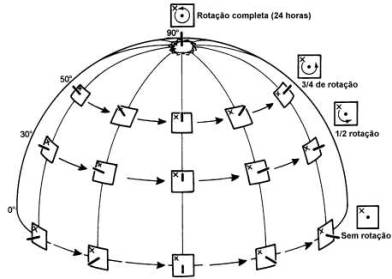
Ilustração da quantidade de rotação de uma superfície horizontal em torno de um

eixo vertical em várias latitudes, num período de 24 horas.

Será que a água na pia gira sempre para o mesmo lado?

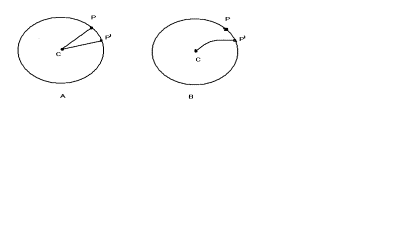
Uma pessoa no centro de um carrossel circular girante lança um projétil em direção ao ponto P na borda desse carrossel. (Veja a figura A abaixo.) Enquanto o projétil viaja, se afastando do centro, o carrossel gira. Assim, ao chegar na borda o ponto P se deslocou e o projétil atinge um ponto P’. A distância entre P e P’ pode ser deduzida facilmente. Suponha que a velocidade do projétil seja v; se o raio do carrossel for igual a r, o tempo que demorará para o projétil chegar a sua borda é t=r/v. Durante esse tempo a borda do carrossel terá se deslocado de uma distância d=w × r× r/v, onde w é a velocidade angular do carrossel, medida em radianos por unidade de tempo; essa distância será a distância entre P, o ponto mirado, e P’, o ponto atingido pelo projétil medida ao longo da periferia do carrossel.

Assim, observado pelo atirador no centro do carrossel, o projétil parece ter feito uma curva, como sugerido na figura B, desviando-se da direção original.

Esse efeito é típico de movimentos observados a partir de um referencial girante. Quando ocorre na Terra, um referencial girante, seu nome é efeito de Coriolis, homenagem ao pesquisador francês que estudou-o em meados do século passado.

O efeito de Coriolis é observado de forma significativa, na Terra, apenas em grandes movimentos de ar na atmosfera, em movimentos de rios, ou em outras situações que envolvem grandes deslocamentos. Em balística, onde a precisão final é importante, o efeito de Coriolis também deve ser considerado. (E se você analisar o que ocorreria com o projétil na situação descrita acima, você verá que o efeito tem direção oposta nos hemisférios norte e sul.)