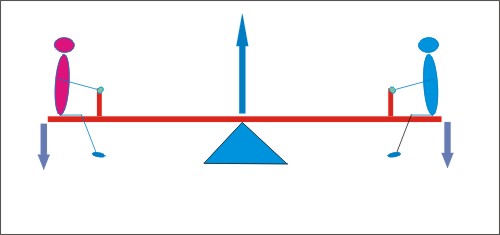
A gangorra está presente
em praticamente todos os parques de diversão. Pense na questão:
duas criança estão sobre a gangorra, como mostra a figura.
Como eles farão para a gangorra executar um movimento de subida e
de descida?
A gangorra
Qualquer criança que já brincou numa gangorra com seus colegas
de diferentes tamanhos sabe que a melhor brincadeira ocorre para duas crianças
que possuem o mesmo tamanho.
Figura 1
Quando duas crianças de pesos iguais estão sentadas nas extremidades
de uma gangorra, então a gangorra esta balanceada.
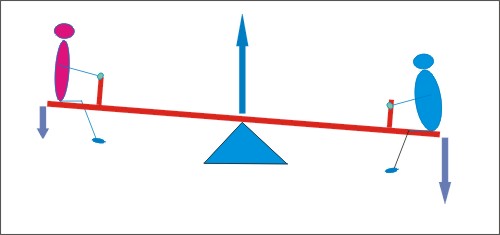
Figura 2
Quando as massas não são iguais, a criança de maior
peso executa movimento descendente.

Figura 3
Se a criança pesada aproximar-se a uma certa distancia do pivô,
a gangorra esta em equilíbrio.
Existem algumas
soluções para o problema da criança gorda e da criança
magra. Primeiramente, nos precisamos entender a natureza do movimento
rotacional. Por simplicidade, vamos ignorar a massa e o peso da gangorra.
Existem então três forças atuando sobre a gangorra como
mostra a figura 1: duas forças para baixo (peso das crianças)
e uma para cima (a forca do suporte do pivô central). Todo movimento
de um objeto de um lugar para outro é denominado movimento de translação.
Um carro andando é exemplo de um movimento de translação.
O movimento em torno de um ponto fixo é chamado de movimento rotacional.
Os ponteiro do relógio executam um movimento rotacional.
É o
movimento rotacional que torna a gangorra interessante, mas, o que faz a
gangorra girar e que observações podem ser feitas sobre
o processo de rotação? Para responder essas questões,
nós precisamos examinar algumas novas quantidades físicas associadas
com a rotação e explorar o movimento rotacional. O movimento
translacional e o rotacional apresentam algumas similaridades. As leis do
movimento rotacional são generalizações feitas do movimento
translacional.
Clique
na figura abaixo para ver uma simulação muito interessante....
Faça a sua aposta....
 O movimento de uma gangorra
isolada
O movimento de uma gangorra
isolada
O conceito de inércia rotacional é semelhante ao de inércia
translacional. Para descrever a inércia rotacional e o movimento rotacional
nós precisamos identificar as quantidades físicas associadas
ao movimento rotacional. A posição angular descreve a posição
da gangorra em relação a uma orientação
de referência. A unidade SI da posição angular e
o radiano. Se a gangorra esta rotacionando a posição
angular esta variando, existe a velocidade angular. A velocidade angular
define a velocidade de rotação da gangorra. A velocidade angular
é definida como:
Velocidade angular = variação
da posição angular
tempo
A unidade Si da velocidade angular e o radiano por segundo.(1/s).
A direção da velocidade angular e definida pela regra da mão
direita. Podemos agora descrever o movimento rotacional de uma gangorra livre.
A primeira lei de Newton do movimento rotacional afirma que um objeto
rígido que não esta oscilando e não esta sujeito a torques
rotacionais externos possui uma velocidade angular constante, percorrendo
ângulos iguais em espaços de tempos iguais em torno de um eixo
de rotação.
Como uma
gangorra responde aos torques
O momento de inércia é a medida da inércia rotacional
de um objeto, a sua resistência à mudança da velocidade
angular. Momento de inércia é análogo à massa,
que é a medida da inércia translacional de um objeto. O momento
de inércia depende de como a massa esta distribuída em torno
do eixo de rotação.
A unidade SI do momento de inércia e o kilograma-metro2
( Kg.m2).
O torque possui módulo e sentido. Quanto maior o torque que se exerce
na gangorra, maior será a mudança da velocidade angular. A
unidade SI do torque é N.m. Para definir o sentido o torque
utiliza-se a regra da mão direita. A aceleração angular
mede como a velocidade angular varia. Quando aplicamos um torque, a aceleração
angular varia.
T = I.a - Segunda Lei de Newton do movimento rotacional
O torque exercido sobre um objeto é igual ao produto do momento de
inércia pela aceleração angular.
Esta equação é parecida com a 2ª lei de Newton
do movimento translacional (F = m.a). Esta nova lei não se
aplica para objetos oscilando porque ele é afetado por mais de um
momento de inércia simultaneamente. No equilíbrio os torques
são iguais.
Torque
Para modificar a velocidade angular da gangorra você precisa exercer
um torque. Mas como podemos exercer um torque? Você coloca sua mão
em uma extremidade da gangorra e aplica uma forca para baixo (ver figura).
Se você aplicar a forca sobre o pivô não haverá
aceleração angular. Se você aplicar uma forca ao longo
da barra da ganogrra, você vai exercer um torque. Se você está
a uma distancia do pivô e aplica uma forca para baixo, você faz
a gangorra girar. Quanto maior a distancia ao pivô, mais facilmente
você ira modificar a velocidade angular.

A distância
do pivô até o lugar onde se aplica a forca é denominado
braço da alavanca (r). Nossa primeira observação
a respeito do torque com a forca é a seguinte. o torque e proporcional
a forca e proporcional ao braço da alavanca.
T = r x
F
Vantagem
mecânica
O valor do torque que uma criança produz na gangorra depende da distancia
até o pivô. Se a criança senta na gongorra sobre o pivô
ela não produz torque. Se ela sentar na extremidade da gangorra, o
torque será o maior possível. Ela pode ajustar seu torque movendo-se
pela gangorra, variando assim a sua distancia ao pivô.
A vantagem mecânica permite que uma pequena força cause grande
torque ao sistema.
Para ver como a vantagem mecânica aparece na gangorra, pense o que
acontece quando duas crianças sentam nas extremidades da gangorra.
Se cada uma pesa 200 N e estão sentada a 2 m de distância do
pivô, então cada uma exerce um torque de 400 N.m. Como esses
torques tem direções opostas, o torque resultante sobre a gangorra
é zero e a gangorra continua em equilíbrio.
Se você colocar uma criança de 400 N a uma distancia de 1m e
uma outra de 200 N a uma distancia de 2 m, a gangorra estará em equilíbrio.
Cada uma exerce um torque de 400 N.m em sentidos opostos.
Exercício resolvido
Um carro de 10.000 N esta localizado a uma distância de 2 m do pivô.
A distância do pivô uma pessoa de 1.000 N deve ficar para a gangorra
estar em equilíbrio?
Este problema e um exemplo da vantagem mecânica.
Tcarro = Tpessoa
Fcarro * Rcarro=Fpessoa * Rpessoa
10000*2=1000*r
r = 20 m.
volta ao topo da página